我们在接触到具体的机器学习算法前,其实很有必要对优化问题进行一些了解。 随着学习的深入,越来越发现最优化方法的重要性,学习和工作中遇到的大多问题都可以建模成一种最优化模型进行求解,比如我们现在学习的机器学习算法,大部分的机器学习算法的本质都是建立优化模型,通过最优化方法对目标函数(或损失函数)进行优化,从而训练出最好的模型。
最常见的最优化方法有梯度下降法、牛顿法和拟牛顿法、共轭梯度方向法等。 在大学课程中,数值分析是计算机或数学相关专业一门比较重要的一门课程,笔者也在大学时自学过相关课程,其介绍的诸多对理论的计算机实现方法,对现在的学习依然发挥着很大的作用。
当然优化算法只是数值分析课程中涉及一部分内容,这一节主要介绍和回顾梯度下降法
梯度下降法
梯度下降法是最为常见的最优化方法。梯度下降法实现简单,当目标函数是凸函数时,梯度下降法的解是全局解。 在一般情况下,其解不能保证是全局最优解,梯度下降法的速度也未必是最快的。
假设$f(x)$是$R^n$上具有一阶连续偏导数的函数,需要求解的无约束最优化问题是:
$${min}_{x\in R^n}:\quad f(x)$$
梯度下降法是一种迭代算法,选取适当的初值$x_0$,反复迭代,更新$x_{i}$的值,进行目标函数的极小化,直至收敛。

由于我们都知道梯度方向$∇f(x)$是函数增长最快的方向,那么自然而然的想到负梯度方向就是函数值下降最快的方向了。因此,我们以负梯度方向作为极小化的下降方向,在迭代的每一步,以负梯度方向来更新$x$的值,从而达到减小函数值目的,这种方法就是梯度下降法。
由于$f(x)$具有一阶连续偏导数,若第k次迭代值为$x_k$,则可将$f(x)$在$x_k$处进行一阶泰勒展开: $$f(x)=f(x^{(k)})+g_k^T(x−x^{(k)})$$ 这里,(方便推广,使用矩阵形式)$$g_k=g(x^{(k)})=∇f(x^{(k)})g_k=g(x^{(k)})=∇f(x^{(k)})$$为$f(x)$在$x_K$的梯度。 第$K+1$次迭代值$x_{k+1}$:即 $$x_{k+1}=x_{k}+λ_k*p_k$$ 其中,$p_k$是搜索方向,梯度法中$p_k=-∇f(x)$,取负梯度方向$p_k=−∇f(x^{(k)}),{\lambda_k}$是步长,有时候我们也叫学习率,这个值可以由一维搜索确定,目的在于得到最合适的步长,即${\lambda _k}$使得
$$Min:\quad \varphi(\lambda)=f(x^{(k)}+λ_kp^{(k)})$$
算法过程:
1)确定当前位置的损失函数的梯度,对于$(\theta_i)$,其梯度表达式如下:
$$(\frac{\partial}{\partial\theta_i}f(\theta_0, \theta_1…, \theta_n))$$
2)用步长乘以损失函数的梯度,得到当前位置下降的距离,即$(\alpha\frac{\partial}{\partial\theta_i}f(\theta_0, \theta_1…, \theta_n))$对应于前面登山例子中的某一步。
3)确定是否所有的$(\theta_i)$,梯度下降的距离都小于$\varepsilon$,如果小于$\varepsilon$则算法终止,当前所有的$\theta_i,(i=0,1,…n)$即为最终结果。否则进入步骤4.
4)更新所有的$\theta$,对于$\theta_i$,其更新表达式如下。更新完毕后继续转入步骤1.
$\theta_i = \theta_i – \alpha\frac{\partial}{\partial\theta_i}f(\theta_0, \theta_1…, \theta_n)$
举例
下面用线性回归的例子来具体描述梯度下降。假设我们的样本是$(x_1^{(0)}, x_2^{(0)}, …x_n^{(0)}, y_0), (x_1^{(1)}, x_2^{(1)}, …x_n^{(1)},y_1), … (x_1^{(m)}, x_2^{(m)}, …x_n^{(m)}, y_n)$,损失函数如前面先决条件所述:
$$f(\theta_0, \theta_1…, \theta_n) = \sum\limits_{i=0}^{m}(h_\theta(x_0, x_1, …x_n) – y_i)^2$$。
则在算法过程步骤1中对于$\theta_i$ 的偏导数计算如下:
$$\frac{\partial}{\partial\theta_i}f(\theta_0, \theta_1…, \theta_n)= \frac{1}{m}\sum\limits_{j=0}^{m}(h_\theta(x_0^{j}, x_1^{j}, …x_n^{j}) – y_j)x_i^{j}$$
由于样本中没有$x_0$上式中令所有的$x_0^{j}$为1.
步骤4中$\theta_i$的更新表达式如下:
$$\theta_i = \theta_i – \alpha\frac{1}{m}\sum\limits_{j=0}^{m}(h_\theta(x_0^{j}, x_1^{j}, …x_n^{j}) – y_j)x_i^{j}$$
从这个例子可以看出当前点的梯度方向是由所有的样本决定的,加$\frac{1}{m}$ 是为了好理解。由于步长也为常数,他们的乘机也为常数,所以这里$\alpha\frac{1}{m}$可以用一个常数表示。
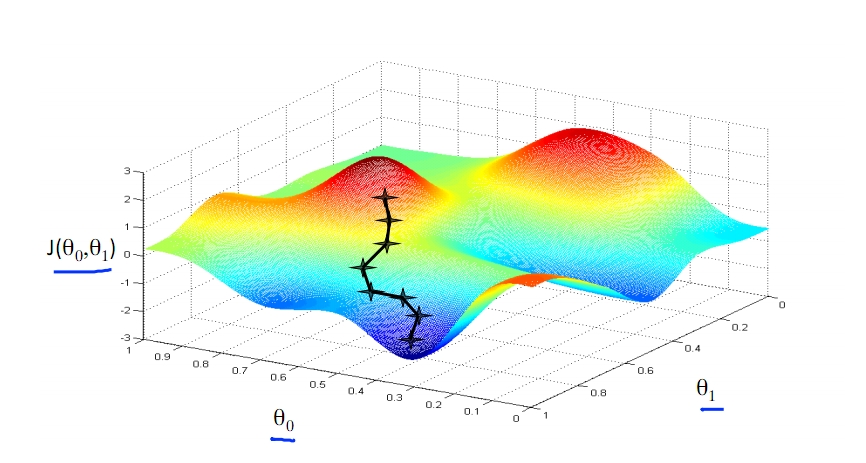
梯度下降法的搜索迭代示意图如下图所示:
参考书籍:
An introduction to optimization-最优化导论[J]. Edwin K.P.Chong.
