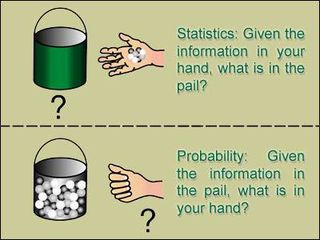
关于概率论与统计学的不同,相信学过统计学的同学,看过上图后一定能秒懂。
统计学:根据手中信息,猜猜桶里有啥?
概率论:根据桶中信息,猜猜手里有啥?
概率空间
所有基本事件组成的集合,其中的每一个基本事件又称做样本点,样本空间用$\boldsymbol {\Omega }$表示,样本点用$\omega$表示,$\Omega=\{\omega \}$
- $\mathcal{\Omega}$-Sample space 样本空间,试验中所有可能结果的集合。(注:每个结果需要互斥,所有可能结果必须被穷举)
- $\mathcal{F}$-Set of events 事件集合,是$\Omega$的一些子集构成的集合,并且它需要满足以下三点特性(也就是必须是$\sigma$-field):
- $\mathcal{\Phi \in F}$(也就是必须包含不可能事件)
- 如果$E\in F,E^C \in \mathcal{F}$。
- 如果$E_1,E_2,\cdots ,E_i \in \mathcal{F}$,那么 $U_{i=1}^{\infty}E_i \in \mathcal{F}$
- $\mathcal{P}$-Probability measure 概率测度(或概率),描述一次随机试验中被包含在 $\mathcal{F}$中的所有事件的可能性。并且它「碰巧」也需要满足三点特性:
- $0\leq P(E_i)\leq 1$(实际限制了总测度为1)
- $P(\Omega)=1$(包含样本空间并且概率为1)
- 如果$E_1,E_2,\cdots ,E_i$是互斥事件,那么$P\{U_{i=1}^{\infty} E_i \}=\sum_{i=1}^{\infty} E_i$
谈斯特林公式
$$n! \sim \sqrt{2\pi }n^{n+\frac{1}{2} }e^{-n} $$
证明见附录,这是概率论中非常重要的理论,基于此可以得到一些精确的数值估计
Stirling与概率问题
什么是一个事件(event)的概率?这是概率论最基本也是争议最多的问题 【例】:抛一枚硬币,出现正面的概率?
这是什么意思,通常认为,将这枚硬币独立的抛「很多次」,那么正面出现的次数「大约」占一半。这是在随机事件中很确定的事。所谓的「平均律」(The law of average)或「大数定律」(The law of large numbers)隐约也是在解释这个说法。现在我们从常识出发,来考虑数学表达。
【问题1】 抛 $2n$ 次硬币,正面恰好出现 $n$ 次的概率又多大? 根据组合学,抛 $2n$ 次硬币,共有 $2^{2n}$ 种可能,假设每一种发生的结果机会均等,那么 $2n$ 次中有 $n$ 次正面的结果共有 $C_{n}^{2n}$种,故得概率为
$p_{2n} = \frac{C_n^{2n}}{2^{2n}} = \frac{(2n)!}{2^{2n}\cdot n!\cdot n!} \qquad (1)$
更有趣的是,当$n$趋向$\infty$时,$p_{2n}$会趋近多少?上述常识性的解释似乎是说, $\lim_{n \to \infty } p_{2n} = 1$,这成立吗?这需要对$(1)$式作精确的估计,于是引出下面的问题
【问题2】当$n$很大时,如何估算?明确地说:当$n$趋向$\infty$时,$n!$的渐进相等式(Asymptotically equal formula)是什么?
即要找一个${a_n}$使得
$$\lim_{n \to \infty} \frac{n!}{a_n} = 1,\quad n! \sim a_n$$
我们希望找到这样的${a_n}$,然后带入$(1)$式中计算极限值 $\lim_{n \to \infty} p_{2n}$,就可以检验上述常识性的说法是否正确。
$n!$的渐进相等式(Asymptotically equal formula)存在吗?如何找? 这时候就需要Stirling公式出场了。
初步否定常识性的概率
现在我们要利用Stirling 公式来探讨概率之谜(the enigma of probability)。
首先观察到一个显然的
【补题】 设$\{a_n\},\{b_n\},\{c_n\}$及$\{d_n\}$皆为正项数列且 $\lim_{n \to \infty} \frac{a_n}{b_n} = l$。若 $a_n \sim c_n$且$b_n \sim d_n$,则 $\lim_{n \to \infty} \frac{c_n}{d_n} = l$。 接着计算「丢$2n$次硬币,恰好出现$n$次正面的机率$p_{2 n}$在 $n \to \infty$的极限」
$$ \lim_{n \to \infty}p_{2n} = \lim_{n \to \infty} \frac{(2n)!}{2^{2n}n!n!} \\ =\lim_{n \to \infty} \frac{\sqrt{2\pi 2n}(2n)^{2n}e^{-2n}}{2^{2n}\cdot 2\pi \cdot n\cdot n^{2n}\cdot e^{-2n}} \\ =\lim_{n \to \infty}\frac{1}{\sqrt{\pi n}}=0 $$
【定理3】 $ \lim_{n \rightarrow \infty} p_{2n} = 0$。 因此,当 $n \to \infty$时,$p_{2n}$不但不如原先预计的趋近于1(即必然发生),反而是趋近于0(即不可能发生)。这警告我们,概率的解释与经验有很大出入。
【常识性的说法】「丢很多次硬币正面大约占一半。」如果将「大约占一半」, 解释为「恰好是一半」的说法,点估计显然是不对的。如何修正呢?自然想到的是改用区间估计的说法。
为了叙述方便起见,我们引入随机变量(random variable)的概念。对于$k =1, 2, 3, \cdots $,令随机变量
$$ f(n) = \begin{cases} \epsilon_k = 1, & \text{第$K$次硬币得到正面 } \\ \epsilon_k = 0, & \text{第$K$次硬币得到反面} \end{cases} $$
再令 $$S_n = \epsilon_1 + \epsilon_2 + \cdots + \epsilon_n$$
这也是一个随机变数,定义在某个机率空间$\mathcal{(\Omega, F , P )}$上,代表丢$n$次硬币中,正面出现次数之随机变数,它具有二项分布。于是「$S_{2 n} = n$」就表示丢$2n$次正面恰好出现$n$次的事件,其概率记为$P ( S_{2 n} = n )$。
因此【定理3】是说。 $\lim_{n \rightarrow \infty} P(S_{2n}=n)=0$
进一步我们猜想:$S_{2n}$落在$n$的附近之概率应该会大起来吧?
也许这是「正面大约占一半」更贴切的解释。精确的计算是探求隐晦奥秘的不二法门,让我们就来算算看。
令$a > 0$唯一个固定数,那么
$$P(n-a \leq S_{2n} \leq n+a) = \sum_{k=n-a}^{n+a} C_{k}^{2n}\cdot \frac{1}{2^{2n} } \\ \sim \frac{2a}{ \sqrt{\pi n}} \rightarrow 0 ,when \quad n \rightarrow \infty$$
因此我们又得到一个不出所料的结果:
【定理4】:对任意固定数$a > 0$, $$\lim_{b \to \infty} P( \mid S_{2n} - n \mid \leq a ) = 0$$
换言之,以$n$为中心,左右之长皆为$a$之区间,概率依然为零! 另外,将偶数$2n$改成奇数$2 n +1$,【定理4】仍然成立。因为当 $n \to \infty$时,相应项的比值为
$$ \frac{ C_{k}^{2n+1}\cdot \frac{1}{ 2^{2n+1} } }{C_{k}^{2n} \frac{1}{2^{2n}}} = \frac {2n+1}{2n+1-k} \cdot \frac{1}{2} \to \frac{1}{2} $$ 所以 $$ P( -a \leq S_{2n+1} - \frac{2n+1}{2} \leq a ) \\ = \sum_{k=-a+ \frac {2n+1}{2}}^{a+ \frac {2n+1}{2}} C_k^{2n} \frac{1}{2^{2n+1}}\\ \sim \frac{1}{2}\sum_{k=-a+ \frac {2n+1}{2}}^{a+ \frac {2n+1}{2}} C_k^{2n} \frac{1}{2^{2n}} \to 0 $$
所以得到 【定理5】:对任意有限正数$a$,恒有 $$\lim_{n \to \infty} P(-a \leq S_{2n+1} - \frac{2n+1}{2} \leq a) = 0$$
将上述【定理4】与【定理5】归结起来就得到:
【定理6】:对任意有限正数$a$,恒有
$$\lim_{n \to \infty} P(-a \leq S_n - \frac{n}{2} \leq a) = 0 $$
这是一个令人惊异的结果,但也令人失望!逻辑的闷棍把常识的观点打得眼冒金星。用任何有限区间$[- a , a\ ]$来网罗住 $S_n - \frac{n}{2}$所散布的概率,当 $n \to \infty$时,根本没有往到任何概率,概率全部流失掉!
换言之,丢$n$次,出现正面的次数,落在包含$\frac{n}{2}$的任何有限区间的机会,当$n$很大时,微乎其微。
什么是概率?它仍然是很神秘!
- 表面来看,Stirling 公式并不漂亮,但却很多用途,它是揭开许多深刻奥秘的钥匙。在研究二项分布的性质时,De Moivre 最先得到这个公式(1718年);后来James Stirling 在1730年又重新得到它。
- $n!$的连续变化就是Gamma函数,内容精彩丰富,这是Euler的贡献。
附录
斯特林公式证明,相当于一道考研题目
$$log{n!}=log{1}+log{2}+\cdots+log{n} $$
因为$\log x$为单调函数,所以
$$\int_{k-1}^{k} \log{x} dx < \log{n!} < \int_{k}^{k+1}\log{x}dx $$ 把上式对$k$从$1$到$n$相加得到
$$\int_{0}^{n}\log{x}dx < \log{n!} < \int_{1}^{n+1}\log{x}dx \qquad(1)$$ $$\Leftrightarrow n\log{n}-n < \log{n!} < (n+1)\log{(n+1)}-n \qquad(2)$$ 这是一个双重不等式,提示我们把$\log {n!}$与两端数的算数平均做比较,即想到$(n+\frac{1}{2})\log{n}-n$ $$d_n=\log{n!}-(n+\frac{1}{2})\log{n}+n \qquad (3)$$ $$d_n - d_{n+1}=\log{n!}-(n+\frac{1}{2})\log\frac{n+1}{n}-1$$ $$\frac{n+1}{n}=\frac{1+\frac{1}{2n+1}}{1-\frac{1}{2n+1}}$$ $\boldsymbol{Taylor}$展开得 $$d_n - d_{n+1}=\frac{1}{3(2n+1)^2}+\frac{1}{5(2n+1)^4}+\cdots $$ 把上式与一个公比的几何级数进行比较得 $$0 < d_n-d_{n+1} < \frac{1}{3\left [ (2n+1)^2-1 \right ]}=\frac{1}{12n}-\frac{1}{12(n+1)}$$ 知是${d_n}$下降序列,说明序列${d_n-(12n)^{-1} }$是上升的,因此,极限$\lim d_n = C$ 存在且有限,但是,由$(3)$知:$d_n \rightarrow C$等价于 $$n! \sim e^C \cdot n^{n+\frac{1}{2} } \cdot e^{-n}$$
这就是斯特林公式的初步证明,其中关于$C$($e^C=\sqrt{2\pi}$)的证明较复杂,有兴趣可参考相关文章,在此不赘述。
