计量模型中关于变量选择,很多同学可能第一个想到的是:前进法,后退法,向前向后逐步回归。但是,这些方法存在一些固有的缺陷,它们会导致某些可能为最优的变量组合无法共同进入模型。
我们抛开传统的统计学教材,把眼光瞄向统计学习理论,就会发现,其实有大量的模型可供我们选择。 今天,先介绍最基础的方法:Lasso。
一、The lasso的提出
Lasso,即Lesat absolute shrinkage and seletion operator.改方法由统计学习领域的执牛耳者Robert Tibshirani于1996年开创。至今为止,这篇文章被引用次数已达14000多次。据说,在学术领域,被引用次数能达到几十次已经可以引以为傲。经过将近20年的发展,这个方法养活了一大群人,同时也发展出了很多更为成熟的理论,如Adaptive lasso,The Grouped lasso,SCAD。
二、The lasso的原理
lasso的思想其实很简单,就是在传统的最小二乘估计上对模型的系数施加一个$L_1$惩罚。 模型形式如下。 $$\widehat{\beta}^{lasso} =\quad argmin_{\beta}\sum_{i = 1}^{N}(y_i - \beta_0 - \sum_{j = 1}^{p}x_{ij}\beta_j)^2 \\ \qquad s. t\sum_{j = 1}^{p}|\beta_j|\leq t.$$
上式等价于
$$\widehat{\beta}^{lasso} = argmin_{\beta}{\sum_{i = 1}^{N}(y_i - \beta_0 - \sum_{j = 1}^{p}x_{ij}\beta_j)^2 + \lambda\sum_{j = 1}^{p}|\beta_j|}$$
看到这个表达式,有没有一种熟悉的感觉?看!
$$\widehat{\beta}^{ridge} = argmin_{\beta} {\sum_{i = 1}^{N}(y_i - \beta_0 - \sum_{j = 1}^{p}x_{ij}\beta_j)^2 + \lambda\sum_{j = 1}^{p}\beta_{j}^2}$$
没错!它其实跟我们在回归分析教材中常见的岭回归(ridge regression)非常相似,只是将$L_2$惩罚换成了$L_1$惩罚。Zou and Hastie在2005年,提出了一种在ridge regression和the lasso之间折衷的方法:the elastic net penalty,思想也非常简单,但是却很有影响力。
回头看下,lasso为何如此流行。 这么做的好处是一举多得的:
- 可以解决岭回归能够解决的问题:多重共线性问题,过拟合问题等;
- 还可以解决岭回归不能解决的问题:将一部分变量的系数压缩至0,即实现变量选择。
我们可以从一张图看出来。
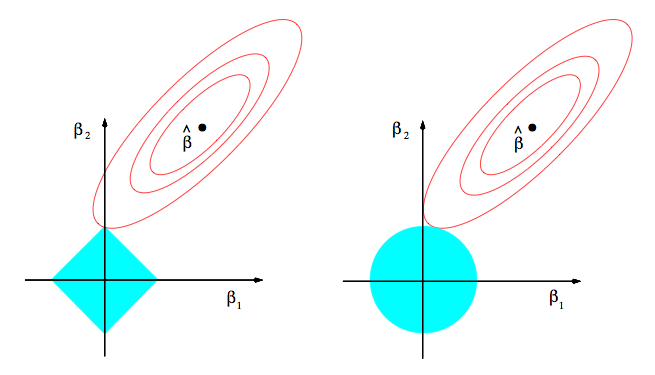
这幅图可以这样理解 蓝色的区域是$\beta$的可行域。由于the lasso的约束是$L_1$约束,必然是方形区域,区域的大小取决于$t$的大小;而ridge regression是$L_2$约束,所以可行域呈圆形。
$$Z = \sum_{i = 1}^{N}(y_i - \beta_0 - \sum_{j = 1}^{p}x_{ij}\beta_j)^2$$
从上面的式子可以看出,(如果我的空间解析几何没记错的话,)函数$Z(\beta_1,\beta_2)$描述的是一个椭圆抛物面的形状。而椭圆抛物面在$(\beta_1,\beta_2)$平面上的投影就是类似上图红色圆圈所表述的形状,每一圈代表着不同的$Z$值。而中间的黑点,自然就是最小的$Z$,即没有约束下,普通最小二乘得到的解。我们可以想象,当蓝色的圆圈足够大,以至于涵盖了中间的小黑点时,约束没有起到作用,取到的解就是中间的小黑点,此时等价于普通最小二乘;当约束比较紧,取到的解靠近0,为两个区域相切的点。
我们可以直观地看到,the lasso更容易取到角点解,即:使得某些变量的系数压缩至零。如果你还是不相信自己的眼睛,我们待会还可以从一个示例中看出这一特点。
一些爱思考的同学可能会继续追问:“它能够保证留下来的变量都是对因变量有着更大影响的吗?”这一点稍微思考一下,应该是可以保证的。但是,如果存在一组高度相关的变量时,Lasso倾向于选择其中的一个变量,而忽视其他所有的变量。这样可能会导致结果的不稳定性。要解决这个问题,可以去探究一下 elastic net penalty。
三、lasso的R实现
lasso的实现可以采用glmnet包。glmnet包作者是Friedman, Hastie, and Tibshirani这三位统计学习领域的大牛,可信度无可置疑。 这个包采用的算法是循环坐标下降法(cyclical coordinate descent),能够处理的模型包括 linear regression,logistic and multinomial regression models, poisson regression 和 the Cox model,用到的正则化方法就是$l1$范数(lasso)、$l2$范数(岭回归)和它们的混合 (elastic net)。
这里,给出一个实现lasso的示例。
数据来源于ISLR包中的Hitters数据集,该数据集描述了美国1986年和1987年的棒球运动员相关数据。我们来探究一下对运动员薪水起主要作用的因素有哪些。
1 | library(ISLR) |
1 | ## 'data.frame': 322 obs. of 20 variables: |
1 | Hitters<-na.omit(Hitters) |
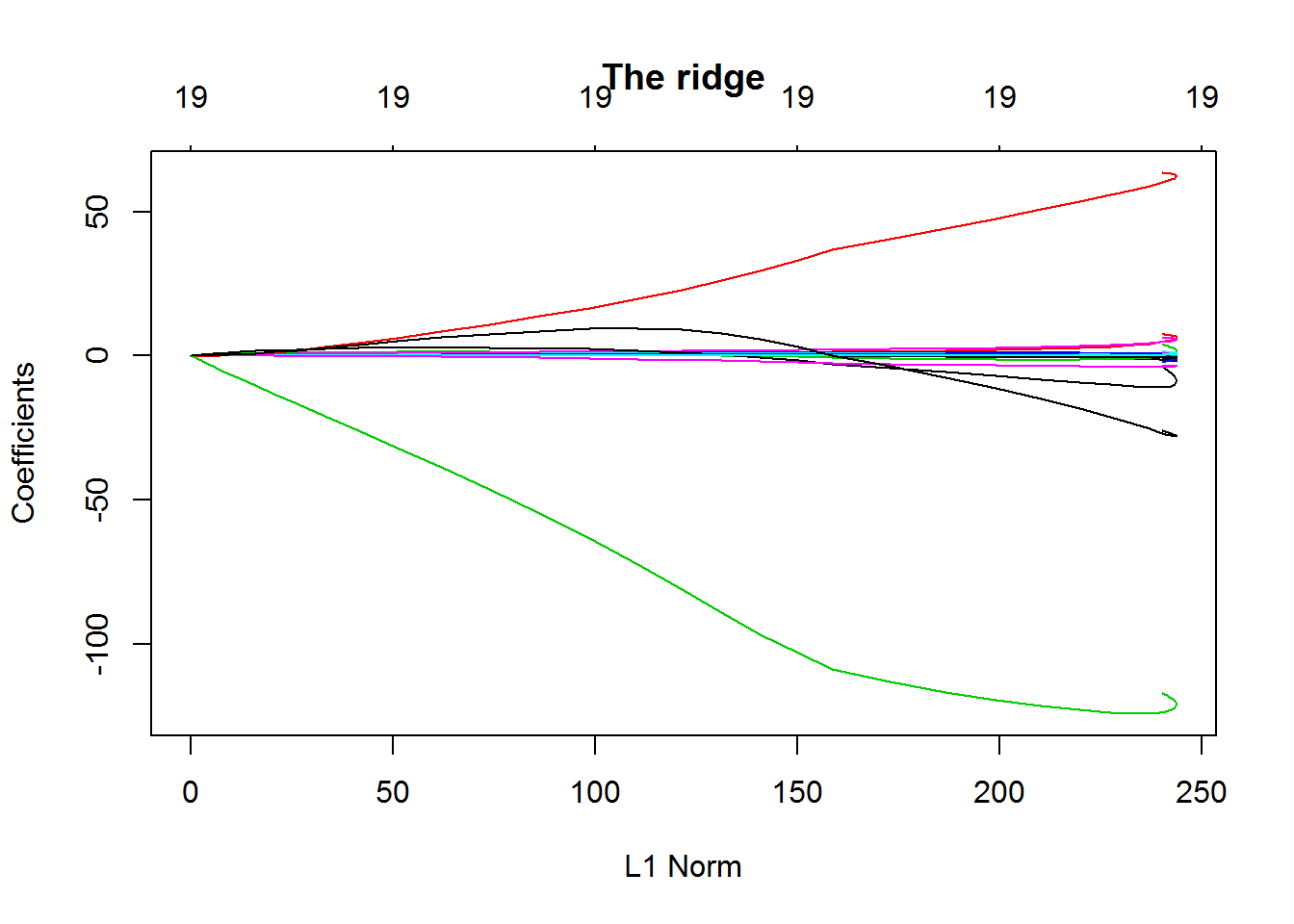
1 | ## the lasso |
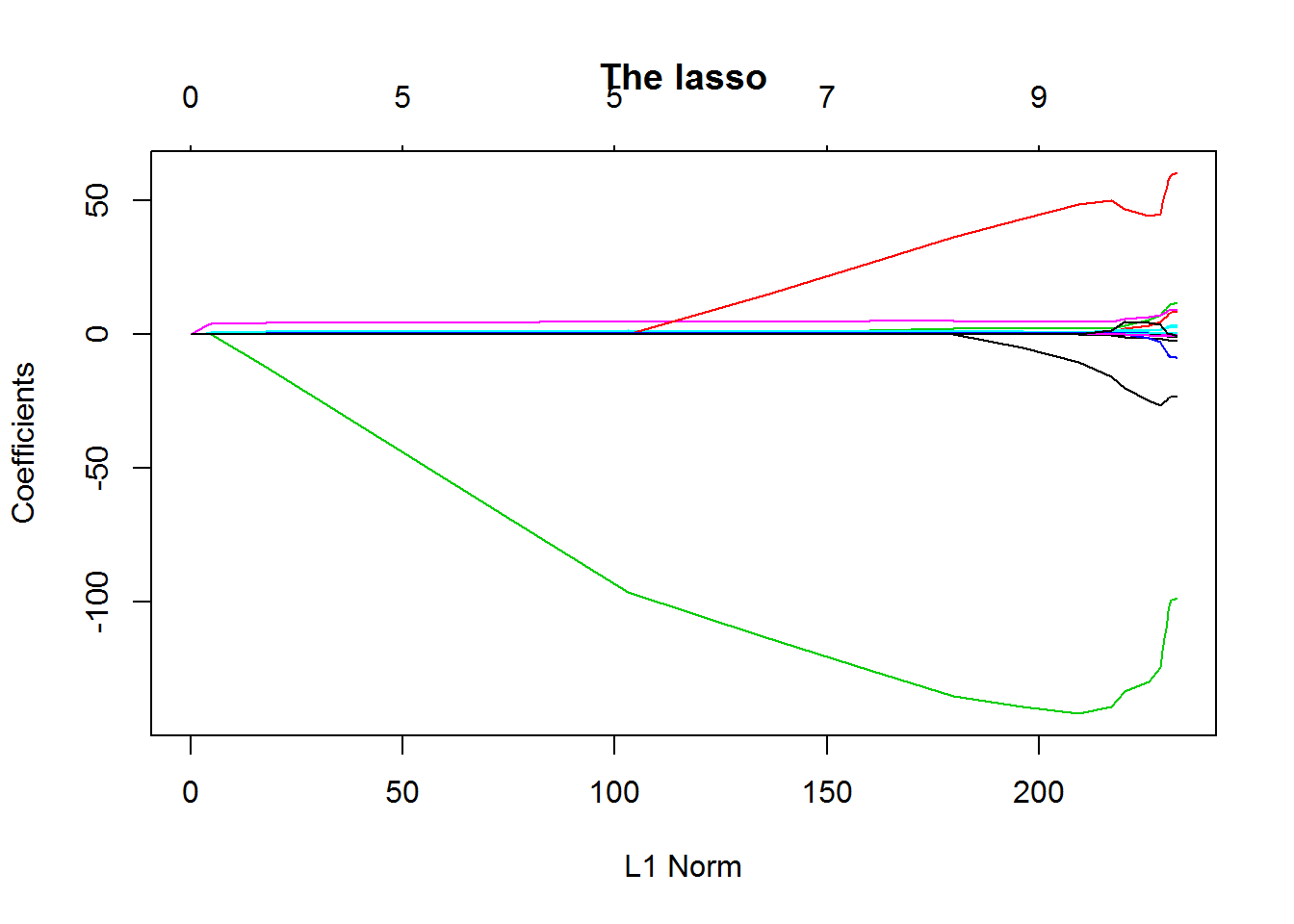
从上面两幅图对比可知,the lasso相比起ridge regression,在压缩变量方便表现更出色。 当然,你还可以使用这个包内部的交叉验证函数对(\lambda)进行参数优化,使得模型更具有稳健性。
1 | ## cross-validation |
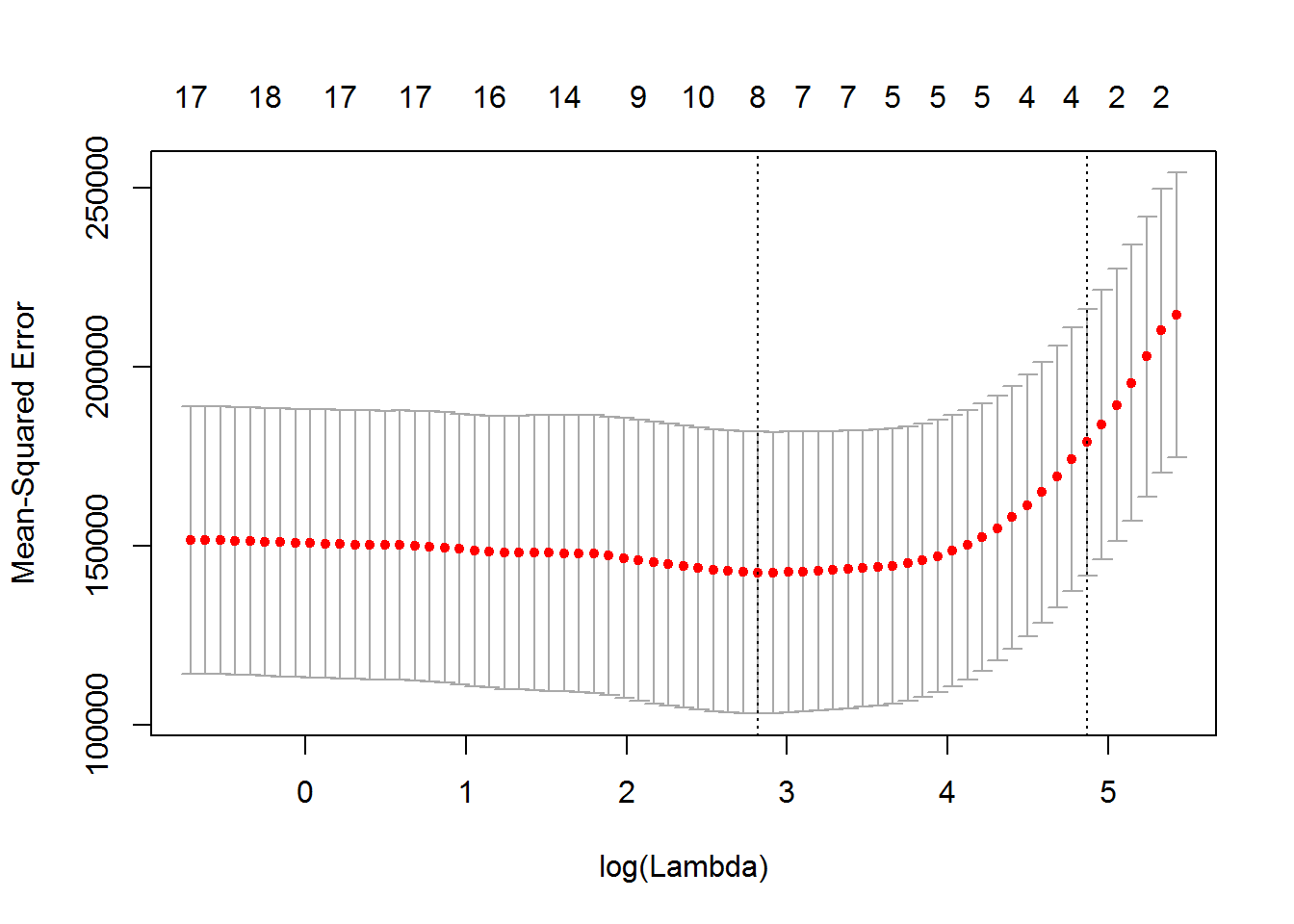
1 | bestlam<-cv.out$lambda.min |
1 | ## [1] 100743.4 |
1 | out<-glmnet(x,y,alpha = 1,lambda = grid) |
1 | ## (Intercept) AtBat Hits HmRun Runs |
可见,很多变量的系数确实被压缩至零。
四、lasso的优缺点分析
- 相比较于其他变量选择方法,如:best subset,Partial Least Squares(偏最小二乘),Principal components regression(主成分回归),the lasso和ridge regression对参数的调整是连续的,并不是一刀切的。
- the lasso相比于ridge regression的优势在于压缩变量表现更出色。
- 但是,正如前面所说,lasso还是会有一些潜在的问题,有时候,elastic net等其他的一些lasso的变形会是更好的选择。
五、参考文献
- The Elements of Statistical Learning: Data Mining, Inference and Prediction. Second edition
- An Introduction to Statistical Learning with R
- 线性回归建模–变量选择和正则化(1):R包glmnet
