目录：
- 说说历史
- Hoeffding不等式
- Connection to Learning
- 学习可行的两个核心条件
- Effective Number of Hypotheses
- Growth Function
- Break Point与Shatter
- VC Bound
- VC dimension
- 深度学习与VC维
- 小结
- 参考文献
VC维在机器学习领域是一个很基础的概念，它给诸多机器学习方法的可学习性提供了坚实的理论基础，但有时候，对我们而言，SVM，LR，深度学习等可能都已经用到线上了，但却不理解VC维。
这里，在台湾大学机器学习基石课程的基础上，我们简单聊聊“VC维的来龙去脉”。我们将解决以下问题：为什么某机器学习方法是可学习的？为什么会有过拟合？拿什么来衡量机器学习模型的复杂度？深度学习与VC维的关系？
说说历史
在讲VC维之前，我们不妨来说说VC维的历史。而说起VC维的历史，又不得不提起神经网络，一方面是因为神经网络与VC维的发明过程是交织在一起的，另一方面是由于神经网络乏善可陈的泛化控制方法，深度学习在理论基础上一直被怀疑，甚至神经网络和VC维的代表SVM还一起争风吃醋过好多年。
- 1943年，模拟神经网络由麦卡洛可（McCulloch）和皮茨（Pitts)提出，他们分析了理想化的人工神经元网络，并且指出了它们进行简单逻辑运算的机制。
- 1957年，康奈尔大学的实验心理学家弗兰克·罗森布拉特(Rosenblatt)在一台IBM–704计算机上模拟实现了一种他发明的叫作“感知机”（Perceptron）的神经网络模型。神经网络与支持向量机都源自于感知机（Perceptron）。
- 1962年，罗森布拉特著作：《神经动力学原理：感知机和大脑机制的理论》（Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms）。
- 1969年，明斯基和麻省理工学院的另一位教授佩普特合作著作：《感知机：计算几何学》（Perceptrons: An Introduction to Computational Geometry)。在书中，明斯基和佩普特证明单层神经网络不能解决XOR（异或）问题。
- 1971年，V. Vapnik and A. Chervonenkis在论文“On the uniform convergence of relative frequencies of events to their probabilities”中提出VC维的概念。
- 1974年，V. Vapnik提出了结构风险最小化原则。
- 1974年，沃波斯（Werbos）的博士论文证明了在神经网络多加一层，并且利用“后向传播”（Back-propagation）学习方法，可以解决XOR问题。那时正是神经网络研究的低谷，文章不合时宜。
- 1982年，在加州理工担任生物物理教授的霍普菲尔德，提出了一种新的神经网络，可以解决一大类模式识别问题，还可以给出一类组合优化问题的近似解。这种神经网络模型后被称为霍普菲尔德网络。
- 1986年，Rummelhart与McClelland发明了神经网络的学习算法Back Propagation。
- 1993年，Corinna Cortes和Vapnik等人提出了支持向量机(support vector machine)。神经网络是多层的非线性模型，支持向量机利用核技巧把非线性问题转换成线性问题。
- 1992~2005年，SVM与Neural network之争，但被互联网风潮掩盖住了。
- 2006年，Hinton提出神经网络的Deep Learning算法。Deep Learning假设神经网络是多层的，首先用Restricted Boltzmann Machine（非监督学习）学习网络的结构，然后再通过Back Propagation（监督学习）学习网络的权值。
- 现在，deep learning的应用越来越广泛，甚至已经有超越SVM的趋势。一方面以Hinton，Lecun为首的深度学习派坚信其有效实用性，另一方面Vapnik等统计机器学习理论专家又坚持着理论阵地，怀疑deep learning的泛化界。
Hoeffding不等式
Hoeffding不等式是关于一组随机变量均值的概率不等式。 如果$X_1,X_2,\cdots,X_n$为一组独立同分布的参数为$p$的伯努利分布随机变量，$n$为随机变量的个数。定义这组随机变量的均值为： $$\bar{X}=\frac{X_1+X_2+\cdots+X_n}{n}$$
对于任意$\sigma > 0$, Hoeffding不等式可以表示为
$$P(|\bar{X}-E(\bar{X})|\geq \sigma) \leq exp(-2{\sigma}^2n^2)$$
更多请参考:Hoeffding不等式，集中不等式
示例:
在统计推断中，我们可以利用样本的统计量(statistic)来推断总体的参数(parameter)，譬如使用样本均值来估计总体期望。如下图所示，我们从罐子里抽球，希望估计罐子里红球和绿球的比例。
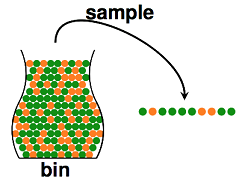直觉上，如果我们有更多的样本(抽出更多的球)，则样本期望$v$应该越来越接近总体期望$\mu $。事实上，这里可以用hoeffding不等式表示如下：
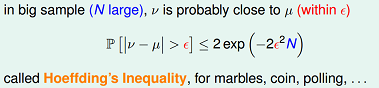从hoeffding不等式可以看出，当$n$逐渐变大时，不等式的UpperBound越来越接近0，所以样本期望越来越接近总体期望。
Connection to Learning
接下来，我们希望可以将机器学习关联到上一节讨论的hoeffding不等式。 一个基本的机器学习过程如下图所示。其中的概念定义为：
- $f$ 表示理想的方案(可以是一个函数，也可以是一个分布)
- $H$ 是该机器学习方法的假设空间
- $g$ 表示我们求解的用来预测的假设，$g$属于$H$
机器学习的过程就是：通过算法$A$，在假设空间$H$中，根据样本集$D$，选择最好的假设作为$g$。选择标准是$g$近似于$f$。
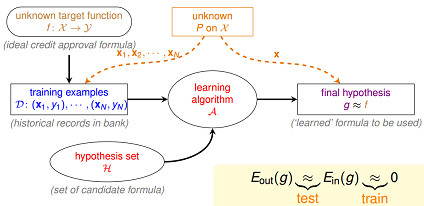
拿感知机(perceptron)来举例。
感知机（perceptron）是一个线性分类器(linear classifiers）。 线性分类器的几何表示：直线、平面、超平面。
perceptron的假设空间，用公式描述，如下所示： $$h(x)=sign((\sum_{i=1}^{n})-threshod)$$
感知器的优化目标如下式所示，$w_g$就是我们要求的最好的假设。 $$W_g\rightarrow argmin\sum_{n=1}^{N}\left [y_n \neq sign(W^Tx_n) \right ]$$
设定两个变量，如下图所示，图中 $f(x)$表示理想目标函数，$h(x)$是我们预估得到的某一个目标函数，$h(x)$是假设空间$H$中的一个假设。 $E_{out}(h)$，可以理解为在理想情况下(已知f)，总体(out-of-sample)的损失(这里是0–1 loss)的期望，称作expected loss。 $E_{in}(h)$，可以理解为在训练样本上(in-of-sample)，损失的期望，称作expirical loss。
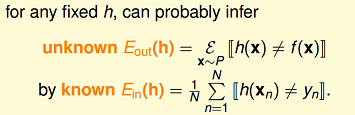
当训练样本量$N$足够大，且样本是独立同分布的，类比于上面“抽球”的例子，可以通过样本集上的expirical loss $E_{in}(h)$ 推测总体的expected loss $E_{out}(h)$。基于Hoeffding不等式，我们得到下面式子：
根据上面不等式，我们可以推断，当$N$足够大时，expected loss和expirical loss将非常接近。
注意在上面推导中，我们是针对某一个特定的解$h(x)$。在我们的假设空间$H$中，往往有很多个假设函数(甚至于无穷多个)，这里我们先假定$H$中有$M$个假设函数。
那么对于整个假设空间，也就是这M个假设函数，可以推导出下面不等式：
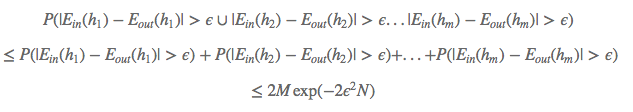
上面式子的含义是：在假设空间$H$中，设定一个较小的$\epsilon$值，任意一个假设$h$，它的$E_{in}(h)$与$E_{out}(h)$的差由该值$2\cdot M\cdot exp{-2\epsilon^2\cdot N}$所约束住。注意这个bound值与 “样本数$N$和假设数$M$” 密切相关。
学习可行的两个核心条件
在往下继续推导前，先看一下什么情况下Learning是可行的?
如果假设空间$H$的size M是有限的，当$N$足够大时，那么对假设空间中任意一个$g$，$E_{out}(g)$约等于$E_{in}(g)$； 利用算法A从假设空间$H$中，挑选出一个$g$，使得$E_{in}(g)$接近于0，那么probably approximately correct而言，$E_{out}(g)$也接近为0；
上面这两个核心条件，也正好对应着test和train这两个过程。train过程希望损失期望(即$E_{in}(g)$)尽可能小；test过程希望在真实环境中的损失期望也尽可能小，即$E_{in}(g)$接近于$E_{out}(g)$。
但往往我们更多在关心，如何基于模型的假设空间，利用最优化算法，找到$E_{in}$最小的解$g$。但容易忽视test这个过程，如果让学习可行，不仅仅是要在训练集表现好，在真实环境里也要表现好。
从上述推导出来的不等式，我们看到假设数$M$在这两个核心条件中有着重要作用。
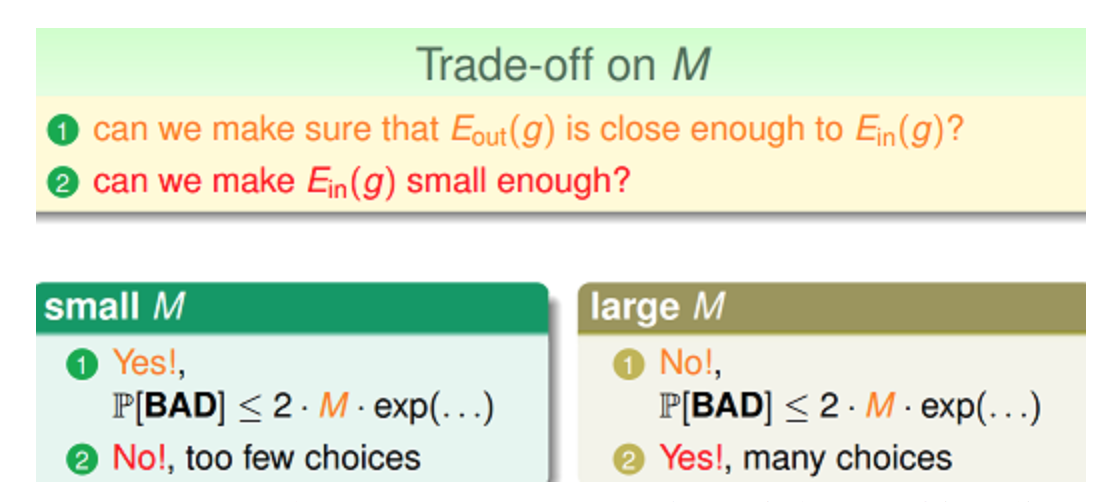
$M$太小，当$N$足够大时，$E_{in}和$E_{out}$比较接近，但如果候选假设集太小，不容易在其中找到一个$g$，使得$E_{in}(g)$约等于0，第二项不能满足。而如果$M$太大，这时候选集多了，相对容易在其中找到一个$g$，使得$E_{in}(g)$约等于0，但第一项就不能满足了。所以假设空间$H$的大小$M$很关键。
对于一个假设空间，$M$可能是无穷大的。要能够继续推导下去，那么有一个直观的思路，能否找到一个有限的因子$m_H$来替代不等式bound中的$M$。
虽说假设空间很大，上述推导里，我们用到了$P(h_1,h_2,\cdots ,h_m) \leq P(h_1) + P(h_2) + \cdots + P(h_m)$。但事实上，多个$h$之间并不是完全独立的，他们是有很大的重叠的，也就是在$M$个假设中，可能有一些假设可以归为同一类。
下面我们以二维假设空间为例，来解释一下该空间下各假设在确定的训练样本上的重叠性。
举例来说，如果我们的算法要在平面上(二维空间)挑选一条直线方程作为$g$，用来划分一个点$x_1$。假设空间$H$是所有的直线，它的size M是无限多的。但是实际上可以将这些直线分为两类，一类是把$x_1$判断为正例的，另一类是把$x_1$判断为负例的。如下图所示：
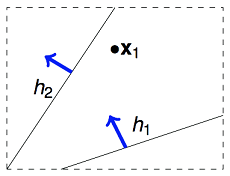
那如果在平面上有两个数据点$x_1,x_2$，这样的话，假设空间$H$中的无数条直线可以分为4类。那依次类推，3个数据点情况下，$H$中最多有8类直线。4个数据点，$H$中最多有14类直线(注意：为什么不是16类直线)。
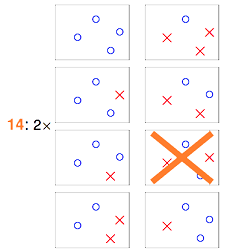从上面在二维假设空间中的分析，我们可以推测到一个结论，假设空间size M是很大，但在样本集$D$上，有效的假设函数数目是有限的。接下来我们将继续推导这个有效的假设函数值。
Effective Number of Hypotheses
对于这个有效的假设函数值，我们尝试用一个数学定义来说明： 从$H$中任意选择一个方程$h$，让这个$h$对样本集合$D$进行二元分类，输出一个结果向量。例如在平面里用一条直线对2个点进行二元分类，输出可能为${1,–1}，{–1,1}，{1,1}，{–1,–1}$，这样每个输出向量我们称为一个dichotomy。
下面是hypotheses与dichotomies的概念对比：
注意到，如果对平面上的4个点来分类，根据前面分析，输出的结果向量只有14种可能，即有14个dichotomies。
如果有$N$个样本数据，那么有效的假设个数定义为： $effective(N) = H$作用于样本集$D$“最多”能产生多少不同的dichotomy。
所以有一个直观思路，能否用$effective(N)$来替换Hoeffding不等式中的M。接下来我们来分析下$effective(N)$。
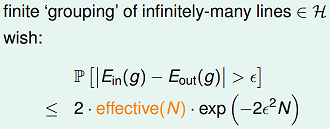
Growth Function
$H$作用于$D$“最多”能产生多少种不同的dichotomies？
这个数量与假设空间$H$有关，跟数据量$N$也有关。将$H$作用于$D$“最多”能产生的dichotomies数量(即effective(N) )表示为数学符号：$max_H(x_1,x_2,\cdots,x_N)$
这个式子又称为“成长函数”(growth function)。在$H$确定的情况下，growth function是一个与$N$相关的函数。
下图举4个例子，分别计算其growth function：
对于第一个例子，positive ray，相当于是正向的射线。该假设空间，作用于1个样本点，可以产生2种dichotomies：(–1)，(+1)。作用于2个样本点，可以产生3种dichotomies：(–1,+1)，(–1,–1)，(+1,+1)。作用于3个样本点，可以产生4种dichotomies。依次类推，可以推导出其成长函数 $m_H(N)=N+1$；
求解出$m_H(N)$后，那是不是可以考虑用$m_H(N)$替换$M$? 如下所示：
$$P[|E_{in}(g)-E_{out}(g)|>\epsilon]\leq 2\cdot m_H(N)\cdot N $$
Break Point与Shatter
在进一步推导前，再看两个概念：shatter，break point。
Shatter的概念：当假设空间H作用于$N$个input的样本集时，产生的dichotomies数量等于这$N$个点总的组合数$2N$是，就称：这$N$个inputs被$H$给shatter掉了。
要注意到 shatter 的原意是“打碎”，在此指“$N$个点的所有(碎片般的)可能情形都被H产生了”。所以$m_{H}=2N$的情形是即为“shatter”。
对于给定的成长函数$m_H(N)$，从$N=1$出发，$N$慢慢变大，当增大到$k$时，出现$m_{H}(N)<2k$的情形，则我们说k是该成长函数的break point。对于任何$N< k$个inputs而言，$H$都没有办法再shatter他们了。
举例来说，对于上面的positive ray的例子，因为$m_H(N)=N+1$，当$N=2$时，$m_H(2)<2^2$， 所以它的break point就是2。
VC Bound
说完break point的概念后，再回到成长函数。 我们将成长函数的上界，设为$B(N,k)$，意为：maximum possible $m_H(N)$ when $break point = k$。
那么我们做一些简单的推导：
- $B(2,2)=3$。因为break point=2，任意两个点都不能被shatter，$m_H(2)$肯定小于$2^2$，所以$B(2,2)=3$。
- $B(3,2)=4$。因为任意两个点都不能被shatter，那么3个点产生的dichotomies不能超过4，所以$B(3,2)=4$。
- $B(N,1)=1$。
- $B(N,k)=2^N \quad for \quad N < k$;$\qquad B(N,k)=2^{N–1} \quad for \quad N=k$；
- $B(4,3)=？$去掉其中的一个数据点$x_4$后，考虑到break point=3，余下数据$(x1,x2,x3)$的dichotomies数目不能超过$B(3,3)$。当扩展为$(x1,x2,x3,x4)$时，$(x1,x2,x3)$上的dichotomies只有部分被重复复制了，设被复制的dichotomies数量为$a$，未被复制的数量为$b$。于是有$B(3,3) = a+b; B(4,3) = 2a + b$。因为$a$被复制了，表示$x_4$有两个取值，那么$(x1,x2,x3)$上的$a$应该小于等于$B(3,2)$。所以推导出$B(4,3) = 2a + b \leq B(3,3) + B(3,2)$。 对于任意$N>k$，类推可以得到，$B(N,k) \leq B(N−1,k)+B(N−1,k−1)$
最后利用数学归纳法，可以证明得到下面的bounding function($N>k$)： $$m_H{N}\leq \sum_{i=0}^{k-1}\binom{N}{i}$$
这个式子显然是多项式的，多项式的最高幂次项为：$N^{k–1}$。
所以我们得到结论：如果break point存在（有限的正整数），生长函数$m_{H}(N)$是多项式的。
再重复一遍，$H$作用于数据量为$N$的样本集$D$，方程的数量看上去是无穷的，但真正有效(effective)的方程的数量却是有限的，这个数量为$m_H(N)$。$H$中每一个$h$作用于$D$都能算出一个$E_{in}$来，一共有$m_H(N)$个不同的$E_{in}$。
OK，到目前为止，关于$m_H(N)$的推导结束。回到growth function小节提出的问题，能否用$m_H(N)$直接替换M?
既然得到了$m_H(N)$的多项式上界，我们希望对之前的不等式中$M$进行替换，用$m_H(N)$来替换$M$。这样替换后，当break point存在时，$N$足够大时，该上界是有限的。 $$P[h\in H\quad s.t \quad |E_{in}(h)-E_{out}(h)|>\epsilon]\leq 2 \\m_{H}N\cdot exp(-2\cdot {\epsilon}^2\cdot N)$$
然而直接替换是存在问题的，主要问题是：$E_{in}$的可能取值是有限个的，但$E_{out}$的可能取值是无限的。可以通过将$E_{out}$ 替换为验证集(verification set) 的$E_{in}$来解决这个问题。
下面是推导过程：
最后我们得到下面的VC bound:
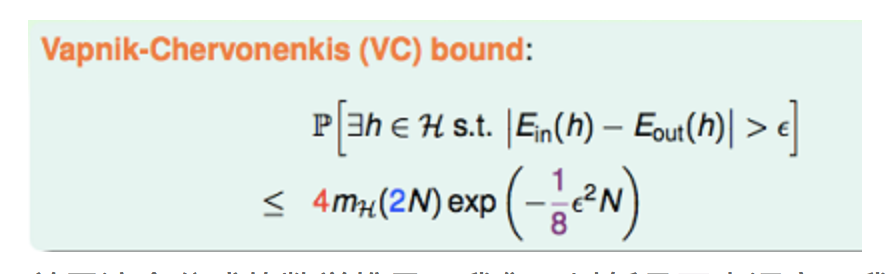
关于这个公式的数学推导，我们可以暂且不去深究。我们先看一下这个式子的意义，如果假设空间存在有限的break point，那么$m_H(2N)$会被最高幂次为$k–1$的多项式上界给约束住。随着$N$的逐渐增大，指数式的下降会比多项式的增长更快，所以此时VC Bound是有限的。更深的意义在于，$N$足够大时，对$H$中的任意一个假设$h，E_{in}(h)$都将接近于$E_{out}(h)$，这表示学习可行的第一个条件是有可能成立的。
VC dimension
说了这么多，VC维终于露出庐山真面目了。此概念由Vladimir Vapnik与Alexey Chervonenkis提出。 一个假设空间$H$的VC dimension，是这个$H$最多能够shatter掉的点的数量，记为$d_{vc}(H)$。如果不管多少个点$H$都能shatter它们，则$d_{vc}=\infty$。还可以理解为：$vc-dim$就是$argmax\quad x_n\quad {growth function=2^n}$。
根据定义，可以得到一个明显的结论： $$k = d_{vc}(H) + 1$$
根据前面的推导，我们知道VC维的大小：与学习算法$A$无关，与输入变量$X$的分布也无关，与我们求解的目标函数$f$ 无关。它只与模型和假设空间有关。
我们已经分析了，对于2维的perceptron，它不能shatter 4个样本点，所以它的VC维是3。此时，我们可以分析下2维的perceptron，如果样本集是线性可分的，perceptron learning algorithm可以在假设空间里找到一条直线，使$E_{in}(g)=0$；另外由于其VC维=3，当$N$足够大的时候，可以推断出：$E_{out}(g)$约等于$E_{in}(g)$。这样学习可行的两个条件都满足了，也就证明了2维感知器是可学习的。
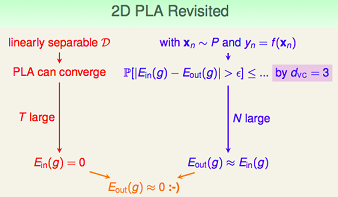
总结回顾一下，要想让机器学到东西，并且学得好，有2个条件：
- $H$的$d_{vc}$是有限的，这样VC bound才存在。(good H)；$N$足够大(对于特定的$d_{vc}$而言)，这样才能保证VC bound不等式的bound不会太大。(good D)
- 算法A有办法在$H$中顺利的挑选一个使得$E_{in}最小的$g$。(good A)
回到最开始提出的学习可行的两个核心条件，尝试用VC维来解释：
从上图可以看出，当VC维很小时，条件1容易满足，但因为假设空间较小，可能不容易找到合适的$g$,使得$E_{in}(g)$约等于0。当VC维很大时，条件2容易满足，但条件1不容易满足，因为VC bound很大。
VC维反映了假设空间$H$的强大程度(powerfulness)，VC 维越大，$H$也越强，因为它可以打散(shatter)更多的点。
定义模型自由度是，模型当中可以自由变动的参数的个数，即我们的机器需要通过学习来决定模型参数的个数。
一个实践规律：VC 维与假设参数$w$的自由变量数目大约相等。$d_{VC} \approx free parameters$。
上面式子中的第3项表示模型复杂度。模型越复杂，VC维大，$E_{out}$可能距离$E_{in}$ 越远。 如下图所示，随着$d_{vc}$的上升，$E_{in}$不断降低，而模型复杂度不断上升。
它们的上升与下降的速度在每个阶段都是不同的，因此我们能够寻找一个二者兼顾的，比较合适的$d_{vc}$，用来决定应该使用多复杂的模型。
模型较复杂时($d_{vc}$ 较大)，需要更多的训练数据。 理论上，数据规模$N$约等于 $10000*d_{vc}$（称为采样复杂性，sample complexity）；然而，实际经验是，只需要 $N = 10*d_{vc}$。
造成理论值与实际值之差如此之大的最大原因是，VC Bound 过于宽松了，我们得到的是一个比实际大得多的上界。
注意在前述讨论中，理想的目标函数为$f(x)$，error measure用的是“0–1 loss”。如果在unknown target上引入噪声(+noise)，或者用不同的error measure方法，VC theory还有效吗？这里只给出结论，VC theory对于绝大部分假设空间(or 加入噪声)和error度量方法，都是有效的。
除此外，我们为了避免overfit，一般都会加正则项。那加了正则项后，新的假设空间会得到一些限制，此时新假设空间的VC维将变小，也就是同样训练数据条件下，$E_{in}$更有可能等于$E_{out}$，所以泛化能力更强。这里从VC维的角度解释了正则项的作用。
深度学习与VC维
对于神经网络，其VC维的公式为：
$d_{VC} = O(V\cdot D)$，其中$V$表示神经网络中神经元的个数，$D$表示weight的个数，也就是神经元之间连接的数目。(注意：此式是一个较粗略的估计，深度神经网络目前没有明确的VC bound)
举例来说，一个普通的三层全连接神经网络：input layer是1000维，hidden layer有1000个nodes，output layer为1个node，则它的VC维大约为$O(1000*1000*1000)$。
可以看到，神经网络的VC维相对较高，因而它的表达能力非常强，可以用来处理任何复杂的分类问题。根据上一节的结论，要充分训练该神经网络，所需样本量为10倍的VC维。如此大的训练数据量，是不可能达到的。所以在20世纪，复杂神经网络模型在out of sample的表现不是很好，容易overfit。
但现在为什么深度学习的表现越来越好。原因是多方面的，主要体现在：
- 通过修改神经网络模型的结构，以及提出新的regularization方法，使得神经网络模型的VC维相对减小了。例如卷积神经网络，通过修改模型结构(局部感受野和权值共享)，减少了参数个数，降低了VC维。2012年的AlexNet，8层网络，参数个数只有60M；而2014年的GoogLeNet，22层网络，参数个数只有7M。
- dropout，drop connect，denosing等regularization方法的提出，也一定程度上增加了神经网络的泛化能力。
- 训练数据变多了。随着互联网的越来越普及，相比于以前，训练数据的获取容易程度以及量和质都大大提升了。训练数据越多，$E_{in}$越容易接近于$E_{out}$。而且目前训练神经网络，还会用到很多data augmentation方法，例如在图像上，剪裁，平移，旋转，调亮度，调饱和度，调对比度等都使用上了。
- 除此外，pre-training方法的提出，GPU的利用，都促进了深度学习。
但即便这样，深度学习的VC dimension和VC Bound依旧很大，其泛化控制方法依然没有强理论支撑。但是实践又一次次证明，深度学习是好用的。所以VC维对深度学习的指导意义，目前不好表述，有一种思想建议，深度学习应该抛弃对VC维之类概念的迷信，尝试从其他方面来解释其可学习型，例如使用泛函空间（如Banach Space）中的概率论。
更多细节请参考下面链接：
- VC Dimension of Multilayer Neural Networks，该文章给出了多层神经网络的VC bound的相关证明。
- Lecun: What is the relationship between Deep Learning and Support Vector Machines / Statistical Learning Theory?Vapnik really believes in his bounds. He worried that neural nets didn’t have similarly good ways to do capacity control (although neural nets do have generalization bounds, since they have finite VC dimension).Lecun’s counter argument was that the ability to do capacity control was somewhat secondary to the ability to compute highly complex function with a limited amount of computation.
小结
上面仔细分析了VC维的来龙去脉，讲述了VC维在机器学习理论中的指导意义。考虑到VC维在机器学习领域虽是基础，却也是大坑，难免有理解不深或不当之处，敬请谅解。若希望获得更深理解，请参考下面的参考文献。
