文章转载自链接

关于空间的紧性,我们在之前的分析中已经见过了:例如在实数轴上的有界闭区间就是典型的紧集,紧集具有很多优良的性质,比如我们知道在有界闭区间上的连续函数一定是一致连续的,并且能取到最大值和最小值。所以,在将空间的概念推广到一般的拓扑空间之后,我们也希望将紧性这一优良性质也带到拓扑空间中来。为此,我们需要找到什么是紧集最本质的东西。在实数轴上的紧集 $K$,有如下的一些等价刻画:
- $K$ 是有界闭集
- $K$ 的任意无限子集必存在极限点
- $K$ 中的任意序列必有收敛子列
- $K$ 的任意开覆盖必有有限子覆盖
其中第一条无法在拓扑空间中使用,因为“有界”的概念无法定义。第二或者第三条曾经被认为是实质性的,但是后来由于 $\text{Tychonoff}$ 定理,人们发现最后一条才是真正好的定义,因此将其作为拓扑空间紧性的定义,而第二条和第三条分别被叫做“极限点紧(Limit point compact)”和“序列紧(Sequencially compact)”。下面是正式内容,在给出定义之前,我先给出一个提纲:
- 首先当然是要给出拓扑空间紧性的定义。
- 接下来当然是会举一些例子,一方面是把枯燥的定义从抽象中拉回来,另一方面也是非常重要的是给出紧空间的存在性的证据,因为定义总是可以随便给的,这样子我可以给出具有任意优良性质的定义来,然而所定义的东西如果是不存在的话,相关的一切性质其实都是空谈。
- 然后我们将介绍从已有的紧空间构造新的紧空间的方法:包括集合的交、并、补,以及子空间、商空间和积空间——这一系列都是标准套路。在这里将会出现一个大定理,就是刚才提到的 $\text{Tychonoff}$ 定理。
- 接下来将暂时中断一下,讨论一下稍微具体一点的度量空间(Metric Space)中的紧性。因为度量空间更加具体一些,所以能得到的性质也更丰富一些。
- 最后我们将简要介绍一些将非紧空间(non-compact space)转化为紧空间(compactification,紧化)的初步知识。
但从度量空间的紧性开始那部分内容并不在这里论述。
定义 1:设 $X$ 是一个集合,它的一族子集 $\mathcal{A}=\{A_\lambda | \lambda\in\Lambda\}$ 如果满足 $$\bigcup_{\lambda\in\Lambda}A_\lambda = X$$ 则称为 $\mathcal{A}$ 为 $X$ 的一个覆盖,或 $\mathcal{A}$ 覆盖 $X$ 。特别地,如果 $X$ 是一个拓扑空间,而且每个 $A_\lambda$,$\lambda\in\Lambda$ 都是 $X$ 中的开集,则称 $\mathcal{A}$ 为 $X$ 的一个开覆盖。
定义 2:拓扑空间 $X$ 称为紧的,如果它的任意开覆盖有有限子覆盖。
其实根据这个定义里的描述,也可以看出紧性之所以好的一些端倪了,不精确地说,利用紧性我们可以把无限的东西转化为有限的情况来处理。
我们最熟悉的紧空间的例子应该就是 $\mathbb{R}$ 中的闭区间了,在数学分析中已经证明过它是紧的。其他我们还可以举一些简单的例子,比如:
- 任意由有限点集所构成的拓扑空间是紧的。因为无论在它上面给怎么样的拓扑,它所有的开集的个数总是有限的,所以任意开覆盖本身就是有限覆盖了。
- 具有余有限拓扑(cofinite topology )的空间是紧的。因为假设 $\mathcal{A}$ 是具有 cofinite topology 的空间 $X$ 的一个开覆盖,从 $\mathcal{A}$ 中任选一个非空的元素 $A_0$,由 cofinite topology 的定义,知道 $X-A_0$ 只有有限个元素 $x_1,\ldots,x_n$ ,对于每一个 $x_i$,$i=1,\ldots,n$ 可以找到一个 $A_i\in\mathcal{A}$ 使得 $x_i\in A_i$ ,这样,${A_0,A_1,\ldots,A_n}$ 就是 $X$ 的开覆盖 $\mathcal{A}$ 的一个有限子覆盖。
非紧空间的例子也很好举,例如 $\mathcal{R}$ 上的区间 $(0,1]$ 就不是紧的,因为我们可以构造一个开覆盖 $\{(1/n,1] \}_{n=1}^\infty$ ,它的任意一个有限子集族总是无法覆盖 $(0,1]$ 。
有了基本的例子之后,下面我们来讨论如何从已有的紧空间构造新的紧空间。从集合的角度来看,构造新的集合常用的操作有 $\cap$、$\cup$ ,从空间的角度来看则有子空间($\iota$)、商空间($\pi$)、积空间($\Pi$),下面我们就依次讨论在这些操作下紧性是否能得到保持。
首先是紧空间的交集,因为任意拓扑空间的交集上,最自然的拓扑就是这一系列包含映射所诱导的始端拓扑(Initial Topology),如果这些拓扑空间互相之间没有什么关系的话,讨论起来就比较复杂了,通常我们会讨论所有要取交的拓扑空间是一个大的拓扑空间的子空间的情况,这个时候它们的交集实际上就是子空间的一种特殊情况,所以我们放到讨论子空间的紧性的时候再讨论。
其次是并集。任意多个并的情况显然是不对的,例如 $\mathbb{R}$ 上可数个紧集 $[n,n+1]$,$n\in\mathbb{Z}$ 的并集是 $\mathbb{R}$ 本身,并不是紧的。不过有限个的情况表现还是良好的。
命题 1:若 $X_1,\ldots,X_n$ 是空间 $X$ 的有限个紧子集,则它们的并也是紧的。
证明:记 $Y=\cup_{i=1}^n X_i$ 。设 $\mathcal{A}={A_\lambda|\lambda\in\Lambda}$ 是 $Y$ 的任一开覆盖,则显然它也是每一个 $X_i$,$i=1,\ldots,n$ 的开覆盖,因此对于每个 $X_i$ ,存在 $\mathcal{A}$ 的一个有限子集族 $\mathcal{A}_i$ 仍然覆盖 $X_i$ 。令 $$ \mathcal{A}’=\bigcup_{i=1}^n \mathcal{A}_i $$
则显然 $\mathcal{A}’$ 是 $\mathcal{A}$ 的一个有限子集族,并且它仍然覆盖 $Y$ 。
接下来我们讨论拓扑子空间的紧性。一个紧空间的子空间是否一定是紧的呢?显然不一定,明显的反例是紧空间 $[0,1]$ 的子空间 $(0,1]$ ,但是如果限制到闭子集的话,就可以做到了:
定理 1:紧空间的闭子集是紧的。
注意这里我们称一个空间的子集是紧的,实际上是在说这个子集配上子空间拓扑之后是一个紧空间。在证明这个定理之前,我们先给一个方便的验证子空间紧性的判定定理:
定理 2:设 $Y$ 是 $X$ 的子空间,$Y$ 是紧的,当且仅当任意一族覆盖 $Y$ 的 $X$ 中的开集包含一个覆盖 $Y$ 的有限子族。
这里的意思是说,如果 $Y$ 是 $X$ 的子空间,判断 $Y$ 的紧性的时候,用 $X$ 中的开集来覆盖还是用 $Y$ 中的开集来覆盖都是一样的。这个定理可以省去我们在验证的时候的一些麻烦。
证明:首先证正向:设 $Y$ 是紧的,$\mathcal{A}={A_\lambda|\lambda\in\Lambda}$ 是一族覆盖 $Y$ 的 $X$ 中的开集,则 $\mathcal{A}’={A_\lambda\cap Y|\lambda\in\Lambda}$ 是 $Y$ 的一个开覆盖,根据紧性,存在有限子覆盖 $$ \{A_{\lambda_1}\cap Y,\ldots,A_{\lambda_n}\cap Y\} $$ 显然对应的 $\mathcal{A}$ 的子族 $$ \{A_{\lambda_1},\ldots,A_{\lambda_n}\} $$ 仍然覆盖 $Y$ 。
再证反过来,设 $\mathcal{A}={A_\lambda|\lambda\in\Lambda}$ 是 $Y$ 的一族开集,它覆盖了 $Y$ ,则根据子空间拓扑的定义,对于每个 $A_\lambda$,$\lambda\in\Lambda$ ,存在 $X$ 中的开集 $U_\lambda$ 使得 $A_\lambda=U_\lambda\cap Y$ ,因此 ${U_\lambda|\lambda\in\Lambda}$ 是一族覆盖 $Y$ 的 $X$ 中的开集,由定理假设,它包含一个有限子族 $$ \{U_{\lambda_1},\ldots,U_{\lambda_n}\} $$ 仍然覆盖 $Y$ ,则对应的 $$ \{U_{\lambda_1}\cap Y=A_{\lambda_1},\ldots,U_{\lambda_n}\cap Y=U_{\lambda_n}\} $$ 是 $\mathcal{A}$ 的一个有限子族,并且仍然覆盖 $Y$ ,由此得 $Y$ 是紧的,即证。
定理 1 的证明:设 $X$ 是紧空间,$K$ 是 $X$ 的闭子集,$\mathcal{A}$ 是 $K$ 的任一开覆盖,则 $$ \mathcal{B}=\mathcal{A}\cup\{X-K\} $$ 是 $X$ 的一个开覆盖,由 $X$ 的紧性,存在 $\mathcal{B}$ 的一个有限子族 $\mathcal{B}’;$ 仍然覆盖 $X$ 。如果 $X-K\in\mathcal{B}’$ 则将它从中去掉,否则不做任何操作,得到 $$ \mathcal{A}’=\mathcal{B}’-\{X-K\} $$ 是 $\mathcal{A}$ 的一个有限子族,并且它是覆盖 $K$ 的。证完。
借助子空间紧性的结论,对于刚才提到的紧集的交的紧性,我们可以有这样一个推论:
推论 1:设 $X$ 是一个拓扑空间,$\{K_\lambda|\lambda\in\Lambda\}$ 是 $X$ 的一族紧且闭的子集。那么它们的交 $\cap_\lambda K_\lambda$ 也是紧的。 由任意闭集的交集是闭集,并且这个交集是其中某一个(任意一个)紧集 $K_\lambda$ 的子集,根据定理 1 立即得到。 接下来我们讨论紧空间的商空间,紧性在这里的表现是很好的,但是我们并不直接给出商空间的紧性,而是叙述一个更一般的结论:
定理 3:设 $f:X\rightarrow Y$ 是连续映射,$X$ 是紧空间,那么 $f(X)$ 也是紧的。 由商映射的连续性以及到上性(满射),根据这个定理立即可以得到任意紧空间的商空间仍然是紧的。
证明:设 $\mathcal{A}=\{A_\lambda|\lambda\in\Lambda\}$ 是 $F(X)$ 的一个开覆盖,则由 $f$ 的连续性知 $$ \mathcal{B}=\{f^{-1}(A_\lambda)|\lambda\in\Lambda\} $$ 是 $X$ 的一个开覆盖。由 $X$ 的紧性,存在 $\mathcal{B}$ 的一个有限子集族 $$ \mathcal{B}’=\{f^{-1}(A_{\lambda_1}),\ldots,f^{-1}(A_{\lambda_n})\} $$ 仍然覆盖 $X$ 。则对应的集族 $$ \mathcal{A}’=\{A_{\lambda_1},\ldots,A_{\lambda_n}\} $$ 是 $\mathcal{A}$ 的一个有限子集族并且仍然覆盖 $f(X)$ 。证完。
由这个定理可以立即得到,如果两个拓扑空间 $X$ 和 $Y$ 是同胚的,其中一个紧那么另一个必定也是紧的。换句话说,紧性是一个拓扑性质。这样的性质通常可以用来方便地区分两个(在同胚意义下)不同的拓扑空间,因为要证明两个空间同胚,只要找出一个同胚映射就可以了,但是要证明两个空间不同胚,则是要证明不可能有同胚存在,通常是一个更加困难的问题,比较好解决的情况通常都用反证法来做了,就是假设同胚,但是又发现两个空间的某个拓扑性质是不一样,就导出矛盾。
例如,用紧性可以证明球面 $S^2$ 和平面 $\mathbb{R}^2$ 是不同胚的。类似地可以证明 $[0,1]$ 和 $(0,1)$ 是不同胚的。
不过,这里既然提到了同胚和连续映射,就正好也说一下紧空间的好处吧(因为我实在不知道这一小部分内容放在哪里讲比较好了)。我们知道从 $\mathbb{R}$ 上的紧集打出去的连续函数一定是一致连续的,一致连续是比连续要强得多的条件,不过在一般的拓扑空间中并不能方便地定义“一致连续”的概念,不过从紧空间打出去的连续映射仍然具有一些良好的性质:
定理 4:设 $f:X\rightarrow Y$ 是连续映射,如果 $X$ 是紧空间,$Y$ 是 Hausdorff 空间,则 $f$ 是闭映射。 闭映射是一个很好的东西,例如我们有一个非常直接的推论:
推论 2:设 $f:X\rightarrow Y$ 是连续的双射,若 $X$ 是紧空间,$Y$ 是 Hausdorff 空间,则 $f$ 是同胚映射。 为了证明定理 4 ,我们再引入另外两个结论,当然它们本身也是相当重要的,因此也是作为定理出现。首先我们要注意到,在一般的拓扑空间中,紧集不一定是闭的(类比 $\mathbb{R}$ 中:有界闭集等价于紧集)。例如最开始我们举的余有限拓扑空间中,任意集合都是紧的,然而只有有限集才是闭的。不过,如果加上了 Hausdorff 条件的话,这一点就可以得到保证了:
定理 5:Hausdorff 空间中的紧子集是闭集。
这个定理的证明过程本身是比较有用的,因此被抽取出来也作为一个定理:
定理 6:设 $K$ 是 Hausdorff 空间 $X$ 中的紧子集,$p\in X-K$ ,则存在 $X$ 中互不相交的开集 $U$、$V$,使得 $K\subset U$ 和 $p\in V$ 。
证明:$\forall x\in K$ ,由 $X$ 的 Hausdorff 性,存在互不相交的开集 $U_x$ 和 $V_x$ ,使得 $x\in U_x$、 $p\in V_x$ 。当 $x$ 取遍 $K$ 时,我们得到 $$ \mathcal{U}={U_x|x\in K} $$ 是 $K$ 的一个开覆盖,根据 $K$ 的紧性,存在 $\mathcal{U}$ 的一个有限子集族 $$ {U_{x_1},\ldots,U_{x_n}} $$ 仍然覆盖 $K$ 。下面令 $$ U = \bigcup_{i=1}^n U_{x_i},\quad V=\bigcap_{i=1}^n V_{x_i} $$ 则 $U$ 和 $V$ 为互不相交的开集,且 $K\subset U$ 、$p\in V$ 。证完。
定理 5 的证明:设 $K$ 是 Hausdorff 空间 $X$ 中的紧子集,我们现在证明 $X-K$ 是开集。对任意的 $x\in X-k$ ,根据定理 6 ,存在 $X$ 中互不相交的开集 $U$、$V$ 使得 $K\subset U$ 、 $p\in V$,因此 $p\in V\subset X-K$ ,即证。
定理 4 的证明:任取 $X$ 中的闭集 $C$ ,由 $X$ 的紧性和定理 1 知 $C$ 是紧集,由 $f$ 的连续性和定理 3 知 $f© $ 是紧的,再由定理 $Y$ 的 Hausdorff 性和定理 5 知 $f© $ 是闭的。即证。
下面我们再回到主线:接下来只剩下积空间的紧性的讨论了。紧性在这里的表现也是优良的,Tychonoff 定理保证了任意一族紧空间的积空间也是紧的。这是一个很要紧的地方,因为我们在最开始列了 4 条 $\mathbb{R}$ 中紧性的刻画,其中末尾 3 条在度量空间中是等价的,然而在一般的拓扑空间中则不行了,那究竟选哪一条作为紧性的定义呢?正是 Tychonoff 定理一锤定音——选择当前的这个定义,可以得到 Tychonoff 定理的结论,而其他的定义则无法做到。
不过,在讲 Tychonoff 定理之前,我们先来看一下有限个紧空间的积空间的紧性。虽然有限个的情况证明方法和 Tychonoff 中任意积的证明完全不一样,但是有限的情况会引出一个本身也很有用的 Tube Lemma ,所以是不容错过的。由于有限积可以由两两积归纳得到,并且我们之后会有更加一般的情况,这里只给出两个紧空间的积空间的描述:
定理 7:若 $X$ 和 $Y$ 是紧空间,则 $X\times Y$ 也是紧的。
证明这个定理需要用到下面的 Tube Lemma :
定理 8 (Tube Lemma):设 $X$ 和 $Y$ 是拓扑空间,其中 $Y$ 是紧的,若 $X\times Y$ 中的任一开集 $N$ 包含了“切片” $x_0\times Y$ ,则存在 $X$ 中 $x_0$ 的开领域 $W$ 使得 $W\times Y$ 也包含在 $N$ 中。 证明过程可以参考下图,图取自 Munkres 的《Topology》
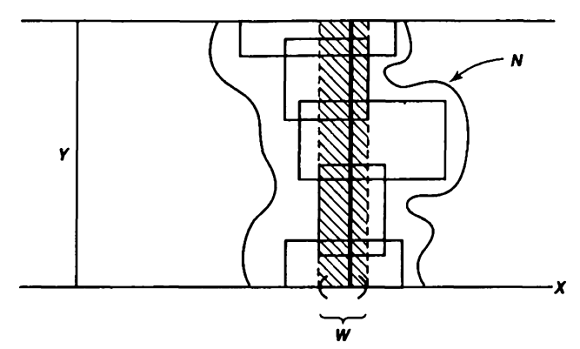
证明:首先,由于 $N$ 是开集,对于每一点 $(x_0,y)\in N$ ,存在其开领域 $N_y\subset N$ ,特别地,我们可以取积拓扑中的基开邻域 $N_y=U_y\times V_y$。令 $y$ 取遍 $Y$ 得到 $x_0\times Y$ 的一个开覆盖。
由于 $x_0\times Y$ 同胚于 $Y$ ,因此是紧的,故存在有限子覆盖。亦即存在有限个点 $y_1,\ldots,y_n\in Y$ ,使得 $$ \mathcal{N}={N_{y_1},\ldots,N_{y_n}} $$ 覆盖 $x_0\times Y$ ,令 $$ W=\bigcap_{i=1}^n U_{y_i} $$ 则 $W\times Y$ 为 $X\times Y$ 中的开集,且 $x_0\times Y\subset W\times Y$ ,下面只需要证明 $W\times Y\subset N$ 即可。任取 $(x,y)\in W\times Y$ ,对应点 $(x_0,y)\in x_0\times Y$ 必定被包含于 $\mathcal{N}$ 中的某一个元素里(有多个的时候任取一个即可),记为 $N_0=U_0\times V_0$ ,则我们有 $y\in V_0$ ,又由于 $x\in W\subset U_0$ ,因此得 $(x,y)\in U_0\times V_0$ ,再由于我们之前取的所有基开邻域 $N_{y}$ 都是包含于 $N$ 中的,因此 $(x,y)\in N$ ,即证。
定理 7 的证明:设 $\mathcal{A}={A_\lambda|\lambda\in\Lambda}$ 是 $X\times Y$ 的任一开覆盖。对任意的 $x_0\in X$ ,$x_0\times Y$ 是紧的,因此可以被有限个元素 ${A_{\lambda_1},\ldots,A_{\lambda_n}}$ 覆盖,记 $$ N=\bigcup_{i=1}^n A_{\lambda_i} $$ 则由 Tube Lemma ,存在 $x_0$ 的开领域 $W$ 使得 $W\times Y\subset N$ ,此时 $W\times Y$ 也被 $A_{\lambda_1}$ 到 $A_{\lambda_n}$ 这有限个 $\mathcal{A}$ 的元素所覆盖。
下面对于每个 $x\in X$ ,可以得到对应的 $W_x$ ,这构成 $X$ 的一个开覆盖 $$ \mathcal{W}={W_x|x\in X} $$ 再由 $X$ 的紧性知道,开覆盖 $\mathcal{W}$ 存在有限子覆盖,亦即存在有限个点 $x_1,\ldots,x_m$ ,使得 ${W_{x_1},\ldots,W_{x_m}}$ 仍然覆盖 $X$ 。因此所有的 tube 构成整个空间: $$ X\times Y = \bigcup_{i=1}^m W_{x_i}\times Y $$ 又由于每个 tube 都可以被有限个 $\mathcal{A}$ 中的元素覆盖,因此整个空间(有限个 tube 的并)可以被有限个 $\mathcal{A}$ 中的元素覆盖。证完。
不过,以上的证明方法只适用于有限积的情况,如果是任意个空间的积空间的话,就没法做了,当然,结论还是成立的:
定理 9 (Tychonoff Theorem):设 ${X_\lambda|\lambda\in\Lambda}$ 是任意一族紧空间,则 $\prod_\lambda X_\lambda$ 是紧的。
要证明这个定理需要做许多准备工作。首先我们将暂时抛开开集,而用闭集来刻画空间的紧性。
定义 3:设 $\mathcal{A}={A_\lambda|\lambda\in\Lambda}$ 是 $X$ 的一族子集,称 $\mathcal{A}$ 满足有限交条件,如果任意有限个 $\mathcal{A}$ 中的元素的交集是非空的。
定理 10:拓扑空间 $X$ 是紧的,当且仅当 $X$ 的任一满足有限交条件的闭集族的交非空。
证明:$X$ 的紧性的定义等价于:对于 $X$ 中的一族开集 $\mathcal{A}$ ,如果 $\mathcal{A}$ 的任意有限子集族都不能覆盖 $X$ ,则 $\mathcal{A}$ 不能覆盖 $X$ 。
将开集族中的每个元素取补集可以得到一族对应的闭子集,因此上面的条件又等价于:对于任意一族闭子集 $\mathcal{A}’$ ,如果 $\mathcal{A}’$ 的任意有限子集族的交非空(满足有限交条件),则 $\mathcal{A}’$ 的交非空。即证。
定义 4:设 $\mathcal{A}={A_\lambda|\lambda\in\Lambda}$ 是 $X$ 的一个开覆盖,称 $\mathcal{A}$ 为 $X$ 的
- 基开覆盖,如果每个 $A_\lambda\in\mathcal{A}$ 属于 $X$ 的某个给定的拓扑基;
- 子基开覆盖,如果每个 $A_\lambda\in\mathcal{A}$ 属于 $X$ 的某个给定的子基拓扑。
为了接下来的叙述方便,下面再定义几个在其他地方不太常用的概念
定义 5:我们称 $X$ 的一族闭子集 $\mathcal{B}$ 为
- 闭基,如果 ${X-B|B\in\mathcal{B}}$ 是 $X$ 的一个基;
- 闭子基,如果 ${X-B|B\in\mathcal{B}}$ 是 $X$ 的一个子基。
定理 11:设 $X$ 是拓扑空间,如下命题等价:
- (1)$X$ 是紧的;
- (2)$X$ 的任一基开覆盖有有限子覆盖;
- (3)$X$ 的任意一族满足有限交性质的闭基集合的交非空。
证明:(1) $\Rightarrow$ (2) 显然。(2) $\Leftrightarrow$ (3) 证明过程和定理 10 的证明完全类似。 (2) $\Rightarrow$ (1) 设 $\mathcal{A}={A_\lambda|\lambda\in\Lambda}$ 是 $X$ 的任一开覆盖,任一 $A_\lambda\in\mathcal{A}$ 都是 $X$ 的一些基开集的并,因此 $$ \mathcal{B}=\{B|B\text{ is base set}, B\subset A_\lambda\text{ for some } A_\lambda\in\mathcal{A}\} $$ 是 $X$ 的一个基开覆盖,由条件,有有限多个 $B_{\lambda_1},\ldots,B_{\lambda_n}\in \mathcal{B}$ 覆盖 $X$ ,在 $\mathcal{A}$ 中取 $A_{\lambda_1},\ldots,A_{\lambda_n}$ 使得 $B_{\lambda_i}\subset A_{\lambda_i}$, $i=1,\ldots,n$ ,则 $\{A_{\lambda_1},\ldots,A_{\lambda_n}\}$ 是 $\mathcal{A}$ 的有限子覆盖。
定理 12 (Alexander Theorem, 1939):设 $X$ 是拓扑空间,如下命题等价:
- (1)$X$ 是紧的;
- (2)$X$ 的任意子基开覆盖有有限子覆盖;
- (3)$X$ 的任意一族满足有限交性质的闭子基集合有非空的交。
证明:
- (1) $\Rightarrow$ (2) 显然。
- (2) $\Leftrightarrow$ (3) 证明和定理 10 的证明完全类似。
- 接下来我们不直接证明 (3) $\Rightarrow$ (1) ,而是证明由本定理的 (3) 可以得到定理 11 的 (3) 。设 $\mathcal{B}={B_\lambda|\lambda\in\Lambda}$ 是 $X$ 中任意一族满足有限交性质的闭基集合,我们要证明它们的交非空。
首先我们来构造一个“极大的”包含了 $\mathcal{B}$ 的具有有限交性质的闭基集族 $\mathcal{C}$。“极大”就是说没有比它更大了,稍后会精确定义,这里的想法是,如果我们能证明这个 $\mathcal{C}$ 的交是非空的,那么自然 $\mathcal{B}$ 的交也是非空的。这看上去好像把问题变难了,因为直观上来讲集族变大之后它们的交集就变小了,所以要保证交集非空就更加困难了。不过,这里的思想大致是将集族扩大到“合适”的程度,使得我们在寻找非空的那个交集的时候没有 $\mathcal{B}$ 那么多的自由度,关键就在于“极大性”上,让我们在构造的时候能做到“恰到好处”。
下面我们用 Zorn’s Lemma 来构造这个 $\mathcal{C}$ ,先令 $\mathbb{B} = \{\mathcal{D}|D$ 是满足有限交条件的闭基集族, $\mathcal{B}\subset\mathcal{D}\}$ 。首先 $\mathbb{B}\neq\emptyset$ ,因为 $\mathcal{B}\in\mathbb{B}$ 。我们以包含关系作为 $\mathbb{B}$ 里的一个偏序,下面证明任意一条链(全序子集)都在 $\mathbb{B}$ 中有上界。
设 $\{\mathcal{D}_k|k\in K\}\subset \mathbb{B}$ 是任意一个全序子集,令 $\mathcal{E}=\cup_k \mathcal{D}_k$ ,则对任意的 $k\in K$ ,$\mathcal{D}_k\subset \mathcal{E}$ 。如果我们证明 $\mathcal{E}$ 满足有限交条件,则 $\mathcal{E}\in\mathbb{B}$ ,显然,它是我们要找的上界。
任取有限个元素 $E_1,\ldots,E_m\in\mathcal{E}$ ,由链的有序性知,存在 $k_0\in K$ ,使得 $E_1,\ldots,E_m \in \mathcal{D}_{k_0}$ ,再由 $\mathcal{D}_{k_0}$ 满足有限交条件,知 $\cap_{i=1} ^m E_i\neq\emptyset$ 。
以上我们证明了 Zorn’s Lemma 的条件是满足的,因此,$\mathbb{B}$ 存在最大元 $\mathcal{C}$ 。下面我们来证明集族 $\mathcal{C}$ 的交非空。
$\mathcal{C}$ 的每个元素是一个闭集集合,由于每个基集合都是有限个子基集合的交,我们有每个闭基集合都是有限个闭子基集合的并。即 $\forall C_\mu \in \mathcal{C}, \mu\in M$ $$ C_\mu = S_1\cap\cdots\cap S_n $$ 这里为了避免下标爆炸,只好乱用一下符号了。实际上对于每个不同的 $\mu$ ,$n$ 是不一样的,而且 $S_1$ 到 $S_n$ 也可能是不同的集合。接下来的下标也会有点乱……现在我们考虑某个特定的 $\mu$ ,如果我们能证明至少存在一个 $i$ 使得 $S_i\in\mathcal{C}$ ,那么对于每个闭基集合 $C_\mu, \mu\in M$ ,取对应的那个 $S_i$ 组成一个集族 ${S_\mu}\subset \mathcal{C}$ ,因此它满足有限交条件,由 (3) 的条件知(注意每个 $S_\mu$ 是闭子基集合),它们的交非空。由此可以立即得到:集族 $\mathcal{C}$ 的交也非空。
最后我们就来证明至少存在一个 $i$ 使得 $S_i\in\mathcal{C}$ ,这里终于要用到 $\mathcal{C}$ 的极大性了。用反证法,假设对任意的 $i=1,\ldots,n$ 都有 $S_i\not\in\mathcal{C}$ 。由于闭子基集合同时也是闭基集合,对于每一个 $i=1,\ldots,n$, 由 $\mathcal{C}$ 的极大性,知道 $$ \mathcal{C}\subsetneq\left(\mathcal{C}_i=\{S_i\}\cup \mathcal{C}\right) $$ 其中 $\mathcal{C}_i$ 必定不能满足有限交条件,亦即,存在 $\mathcal{C}_i$ 的有限子集族 $\mathcal{C}’_i$ (显然 $S_i$ 包含在其中),其交为空集。将所有这些(有限个) $S_i$ 并起来,我们得到 $C_\mu \in \mathcal{C}$ ,而将对应的 $\mathcal{C}’_i$ 交起来,我们得到一个 $\mathcal{C}$ 的子集族 $$ \mathcal{C}_f=\bigcap_{i=1}^n\mathcal{C}’_i $$ 由刚才的构造,知道 $$ C_\mu\cup\left(\bigcap_{C\in\mathcal{C}_f}C\right)=\emptyset $$
而 $\{C_\mu\}\cup \mathcal{C}_f$ 是 $\mathcal{C}$ 的一个有限子集族,这与 $\mathcal{C}$ 满足有限交条件相矛盾。证完。
有了这些准备工作之后,Tychonoff 的证明也就变得简单了:
定理 9 的证明:空间 $\prod_{\lambda}X_\lambda$ 的一族子基是 $$ \{p^{-1}_\lambda(V_\lambda)|V_\lambda\subset X_\lambda, V_\lambda\text{open},\lambda\in \Lambda\} $$ 因此对应的闭子基的每个元素集合是形状如 $$ \prod_{\lambda\in\Lambda}C_\lambda $$ 的集合,其中 $C_\lambda$ 是 $X_\lambda$ 中的闭集(实际上除了最多一个之外,其他的全都是整个空间 $X_\lambda$ )。对于任意一族如上形式的闭子基集族 $\mathcal{A}$ ,如果它们满足有限交性质,我们证明它们的交非空即可。 根据上面的形式可以知道,将 $\mathcal{A}$ 以自然投影投影到任意的 $X_\lambda$ 中,仍然得到一族满足有限交性质的闭集,由 $X_\lambda$ 本身的紧性,知道它们的交非空,因此可以选择其中一点 $x_\lambda$ 。所有的这些点就构成了 $\prod_\lambda X_\lambda$ 中 $\bigcap_{A\in\mathcal{A}}A$ 里的一点 $(x_\lambda)_{\lambda\in\Lambda}$ ,即证。
最后,闲聊一下文章标题图片 Klein Bottle ,课堂上提到拓扑必然会举到的例子,什么橡皮泥啊、克莱因瓶之类的。默比乌斯带还是可以理解的,因为可以做出实物来,但是当时一直觉得克莱因瓶是不对的,所谓顺着瓶子的壁可以从里面爬到外面,我看这各种克莱因瓶的图,都觉得是不对的。到现在终于知道为什么了——确实是不对的,不过不是说 Klein Bottle 不存在,如果用 schematic representation 的话,还是比较可以接受的,只是关于 Klein Bottle 的 visualization ,却是有问题的,因为 Klein Bottle 不能嵌入到 $\mathbb{R}^3$ 中,直观地来说,我们无法在我们生活的三维世界里造出一个克莱因瓶来,如果强行把它放到 $\mathbb{R}^3$ 中,就会出现自相交了,也就是平时所看到的那些图里明显的不对劲的地方了。
不过我比较奇怪,其实用图片来做 visualization 的话,实际上是在 $\mathbb{R}^2$ 中了,结果最大的问题还是出在人类的想象力上吗?不过我觉得这里贴的这张图似乎有点意思了——因为看不太出那么明显的自交。
